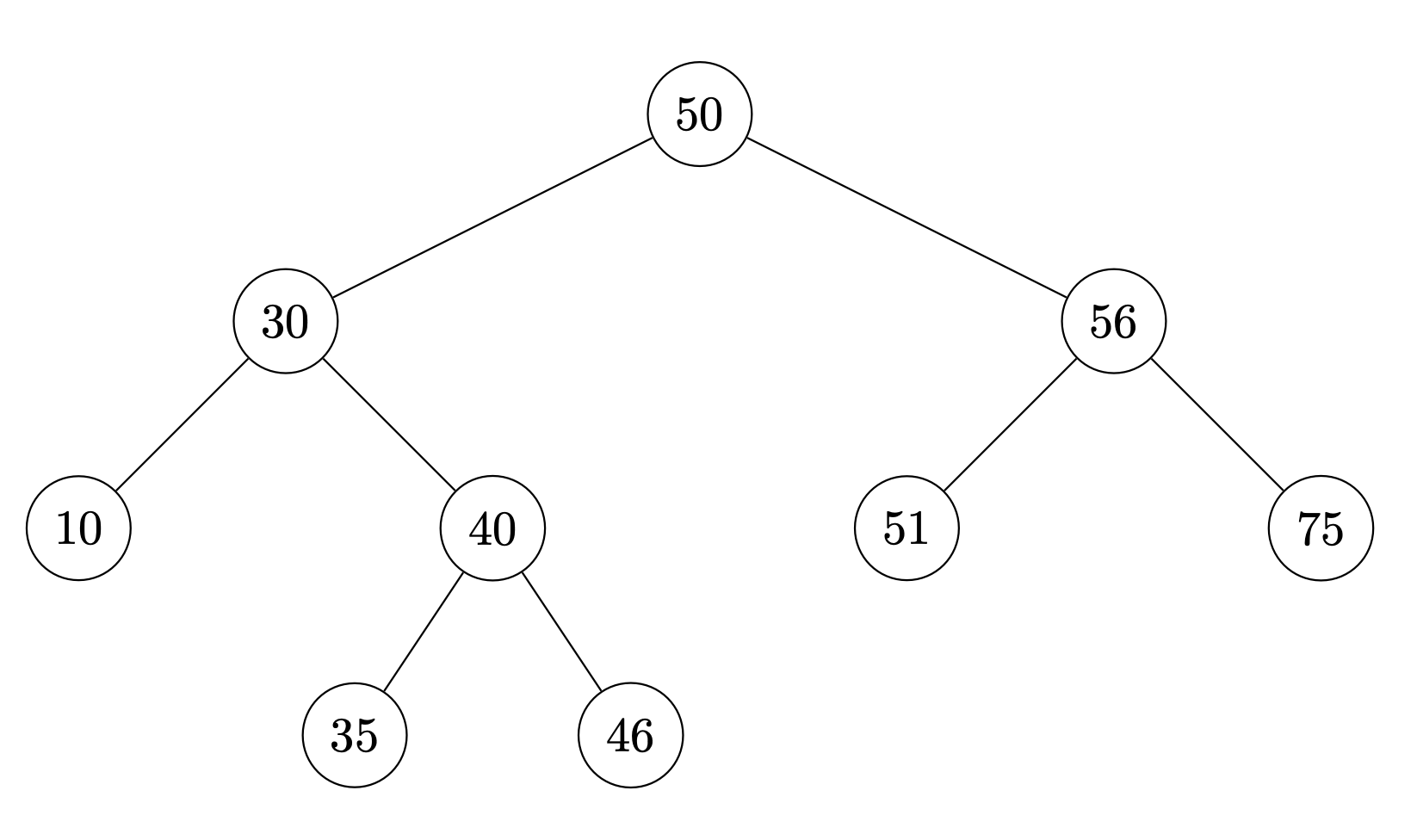
Problem #027
Tags: binary search trees
Suppose the numbers 41, 32, and 40 are inserted (in that order) into the below binary search tree. Draw where the new nodes will appear.
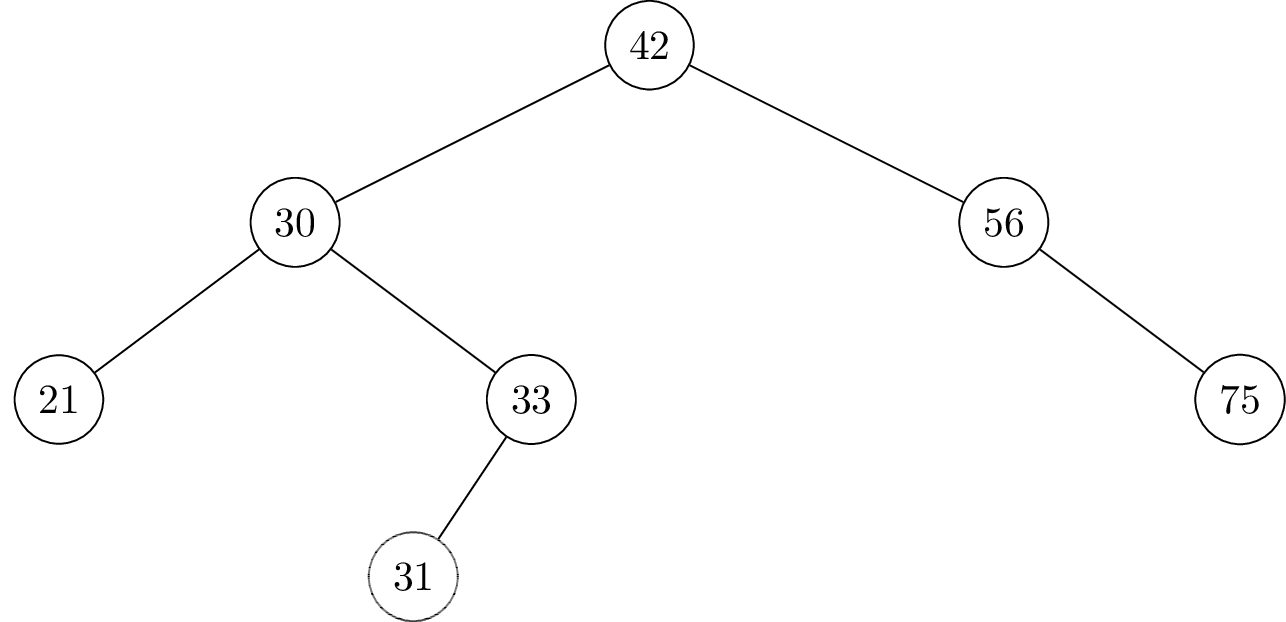
Solution
41 will be the right child of 33.
32 will be the right child of 31.
40 will be the left child of 41.